（播放时建议屏幕最大化并关闭静音）

(一)随机现象。
       在一定条件下，在个别试验或观察中呈现不确定性，但在大量重复试验或观察中其结果又具有一定规律性的现象，称为随机现象。随机现象普遍存在于自然界和现实生活中，例如：投掷一枚硬币，可能正面朝上，也可能反面朝上；同一个工人在同一台机床上加工的同一种零件，其生产出的尺寸不可能完全相同。

(二)统计规律。
         随机现象似乎杂乱无章，但是有偶然性的一面,也有其必然性的一面。在大量次数的重复观察(或试验)中呈现常在某个固定的常数附近摆动，这种规律性我们称之为统计规律性，比如正态分布。二项分布等。
由于随机现象的统计规律必须在大量同类随机现象中才能呈现出来，所以在通过对样本数据进行分析，进而推断总体所呈现的规律时，抽取的样本必须足够多，以充分体现统计规律。

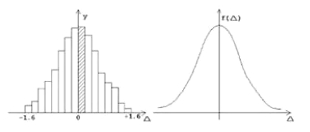
(三)概率论。
         概率论是一门研究随机事件发生可能性的数学分支。概率论是根据大量的同类随机现象的统计规律，对随机现象出现某一结果的可能性从数量上做出一种客观的科学判断，从而形成的一整套数学理论和方法。

(四)数理统计。
         数理统计是概率论的一个分支，研究如何有效地收集、整理和分析随机现象中的数据，确定随机现象中的统计规律，并通过样本对所考察的问题做出推断的科学。
说到这里朋友们可能会觉得统计学难，其实，我们在工作中基本都是借助Minitab软件或者Excel来帮助我们统计计算，我们只需要了解统计技术的应用就可以了，不要让统计学给我们带来过多的畏难心理。

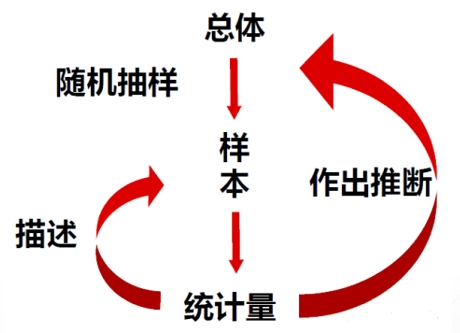
(五)总体和个体。
         在数理统计中，把研究对象的全体称为总体，而把构成总体的每个基本单元称为个体。由于研究的对象可以是一批有限数量的产品，也可以是一连续过程所提供的限数量的产品，所以总体既可以是有限的，也可以是无限的。

         通过全检为手段以确认总体质量的好坏有其限制，尤其是有些产品的功能测试是破坏性的，如车辆的撞击实验，全检将导致产品的破坏。即使是对于非破坏性的测试，全检也是一种浪费。

         为了研究和探讨总体的客观规律，通常从总体中随机抽取n个相互独立的个体进行研究，这n个个体称为总体的一个容量为n的样本。样品要求应该是随机抽样，使总体中的每个个体都有相同的被抽到的机会。

         由于样本不可能完全准确无误地反映整体的特性，因此通过样本推断总体所得出的结论在一定程度上存在着风险。如果错误发生的概率很低，那么根据概率论中的小概率事件原理，概率很小的随机事件在一次试验中几乎不可能发生。

(六)大数定律。
         在抽样推断中，随着样本容量n的增大，抽样平均数x-bar有接近于总体平均数μ的趋势。
大数定律由雅各布·伯努利(1654-1705)提出,他是瑞士数学家、也是概率论的重要奠基人。大数定律提示的是大量试验中随机变量的平均结果具有稳定性的定律。

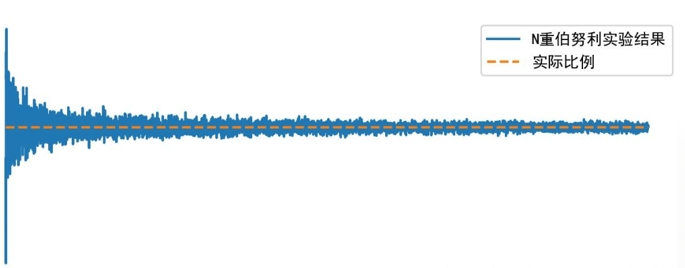
(七)中心极限定律。
         在抽样统计中，如果总体变量存在着有限的平均值和方差，那么不论这个总体的分布如何，随着样本容量n的增大，样本均值的分布总是趋近于正态分布。中心极限定律揭示的是大量随机变量之和的分布是正态分布的规律。

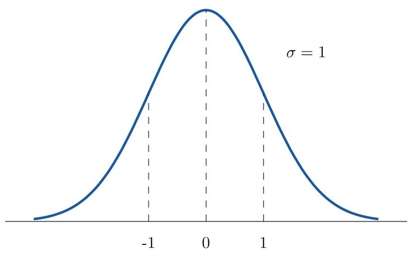
(八)中心值。
         中心值是指一组数据的平均值、中位数和众数，用于表示数据集的集中趋势。

1) 样本均值。
         样本均值是样本数据的算术平均值，它反映了数据的集中位置。

2）中位数。
         将数组中的各值依大小进行排序，在数列中位于中央位置的值称为中位数。当组内数值为偶数时，则以中央两值的算术平均数做为中位数。

3）众数。
         在数组中个数最多的值称为众数。例如：在3,6,6,8,9数组中，6有两个，其他皆为一个，众数为6。

(九)离散程度。
         离散程度是过程控制决定过程稳定程度的一个重要测量数值。在数理统计学中通常以标准差表达一组数据彼此间离散程度的不同，除此外还有几个的重要测量方法：

1）极差。
         极差又称全距，是指一组数据中最大数值与最小数值的差，通常以 R 表示。由于计算极差时仅考虑两个极端值的大小差异，不能顾及中间各个数值，因此，极差相对而言是一个较粗糙的统计数值。

2）平均差。
         是一组数据中各数值与其算术平均数的离差绝对值的算术平均数，通常用MD表示。

3）样本方差s²。

         用样本中每个数据离其均值X-bar的离差平方和除以n-1便是样本方差。之所以除以n-1，是因为n个离差的总和为零，所以对于n个独立的数据为言，独立的离差个数只有n-1个，n-1也称为离差的自由度。

4）样本标准差s。
         样本方差的算术平方根称为样本标准差，又称均方差，是测量变异最主要的指标。在一个统计样本中，其标准差越大，说明它的各个观测值分布的越分散，它的集中趋势就越差。反之，其标准差越小，说明它的各个观测值分布得越集中，它的集中趋势就越好。


例如：计算7个样本23, 24, 28, 34, 23, 22, 21的标准差。
         样本总和 = 23 + 24 + 28 + 34 + 23 + 22 + 21 = 175
         样本均值 x-bar = 样本总和 ÷ 样本数量 = 175 ÷ 7 = 25
         样本方差
         s2 =[(23-25) ²  +(24-25) ²  +(28-25) ²  +(34-25) ²  +(23-25) ²  +(22-25) ²  + (21-25) ²   ] ÷ (7-1) = 124 ÷ 6 = 20.67
         样本标准差 = 20.67的平方根 = 4.55

         下面我们用Excel来操作一遍如何计算样本的平均值和标准差。

1）用AVERAGE函数计算平均值。
         将样本数据分别填写在单元格A1至G1中，然后在H1中输入“=AVERAGE(A1：G1)”，便能计算出平均值。

2）用STDEV函数计算样本标准差。
         将样本数据分别填写在单元格A1至G1中，然后在H1中输入“= STDEV (A1:G1)”，便能计算出样本标准差。

5）离散系数：
         离散系数又称变异系数。常用于对不同的总体进行比对分析，以消除不同总体之间在平均水平、计量单位等方面的不可比因素的影响。离散系数的计算公式为V=总体标准差σ除以平均值乘以100%。

         如果度量单位与平均数相同，可以直接利用标准差来比较。如果单位和（或）平均数不同时，比较其离散程度就不能采用标准差，而需采用标准差与平均数的比值（相对值）离散系数来比较。离散系数同时考虑了中心体大小与标准差，在进行比较分析时，能很直观地判断中心值的代表性。

         一般来说，离散系数越小，说明平均指标的代表性越好；离散系数越大，平均指标的代表性越差。

离散系数对比的缺点有两点：
       (1) 当平均值接近于0的时候，微小的扰动也会对离散系数产生巨大影响，因此造成精确度不足。
       (2) 离散系数只对由比率标量计算出来的数值有意义，也就是说使用区间标量得到的变异系数是没有意义的。