xi 和 yi 是分别来自 N(μ 1 ,σ1²)和N(μ 2 ,σ2²)的样本观测值,要检验这两个分布的均值是否一致。采用处理方法:
令 di =xi - yi (i=1,2,...,n),那么可以把它们看成是来自如下正态总体的样本观察值:
D=X - Y ~ N(μ 1 - μ 2 ,σ1² - σ2² ),记: N(μ ,σ²)
则检验 μ 1 与 μ 2 是否相等的问题就转化为检验假设:
H0 :μ=0 , H1 :μ≠0
这是单个正态总体均值是否零的检验问题。
由于 σ 未知,因此对此问题用 t 检验,检验统计量为:
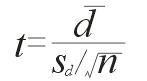
例5-8
某儿童运动鞋制造商希望了解两种鞋底的材料的耐磨性能,于是随机地选择了10名同样年龄的儿童试穿,同一双鞋的左右脚分别使用不同的鞋底材料制作。问两种材料的耐磨性结果在α=0.005水平上有无显著差异:
解题:
这里的数据属于配对数据,每次测定的结果不仅与材料有关,还与孩子的运动习惯有关,xi - yi (i=1,2,...,n)便是两种鞋底材料的差异,n=10。
法1:对差值进行单样本均值是否为零的检验。
Minitab计算路径:统计-->基本统计量-->单样本 t
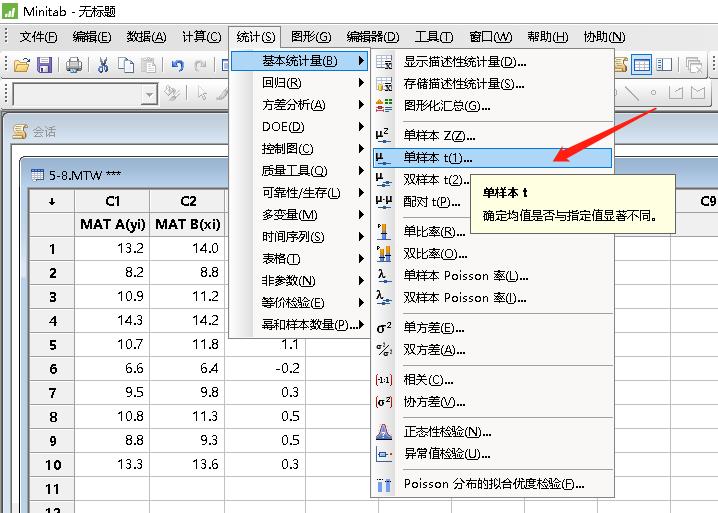
对话框和选项设置:
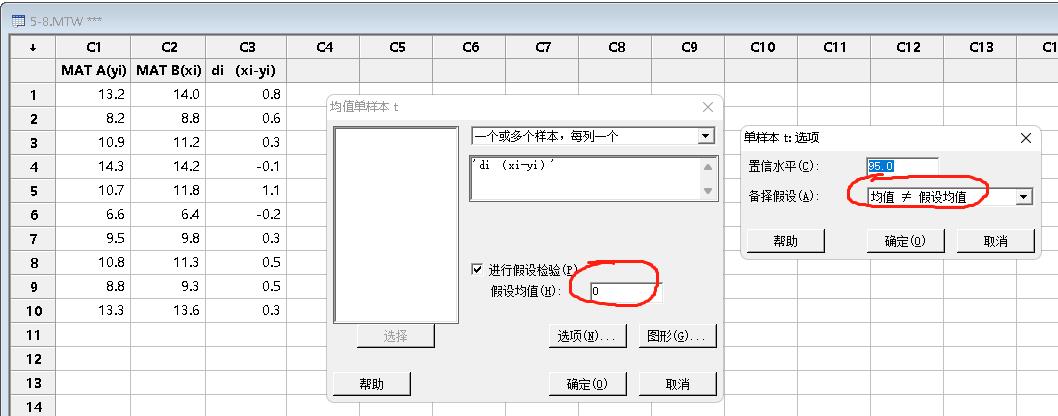
计算结果:
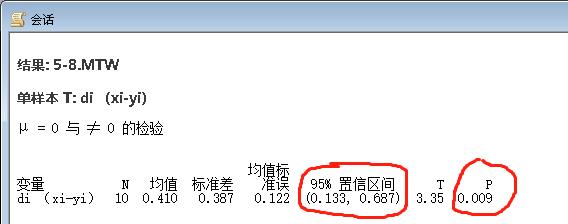
结果分析:P值=0.009<0.05,拒绝原假设,认为测量结果有显著差异。
法2:用配对T检验。
Minitab计算路径:统计-->基本统计量-->配对 T
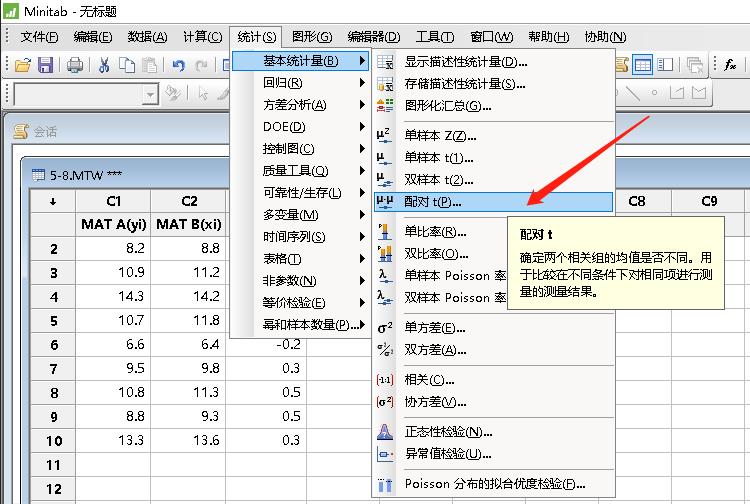
对话框和选项:
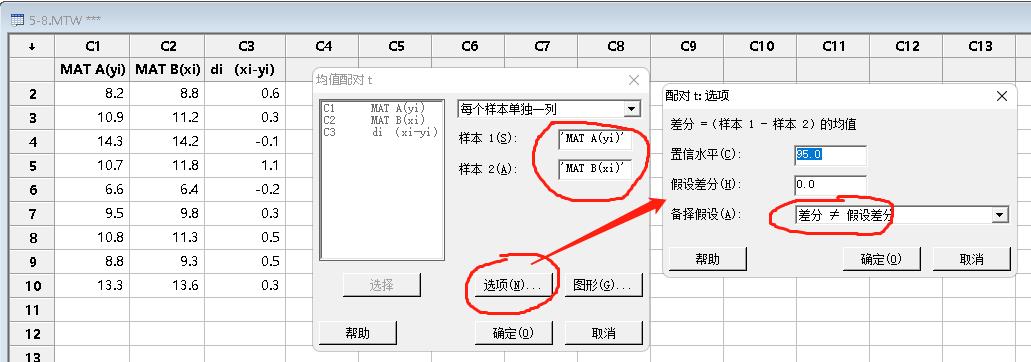
计算结果:

运算结果显然和法1一致。
由于数据表上有两列数据,一些学员容易当做双样本 t 检验不操作,如果我们操作一下看看结果是否一致。
Minitab计算路径:统计-->基本统计量-->双样本 T

对话框和选项设置:
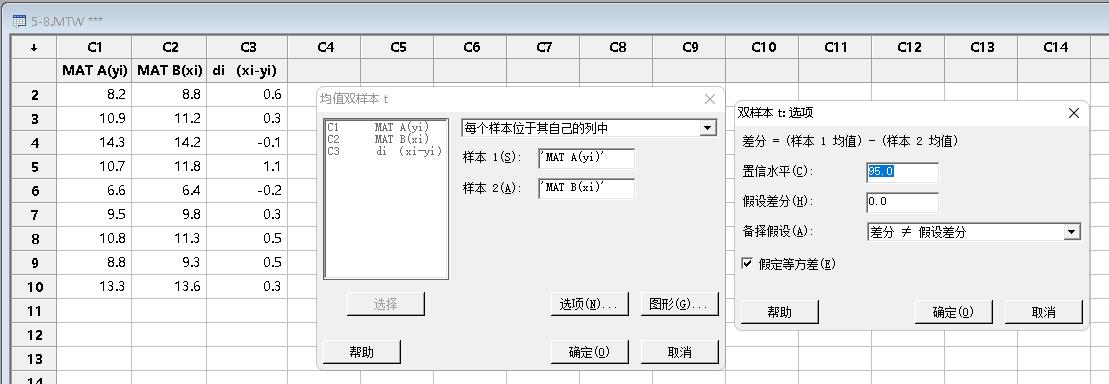
计算结果:

结果分析:
P值=0.717>0.0.5,无法拒绝假设,即不能认为测量结果有显著差异。
相同数据采取配对T和双样本T检验得到的计算结果截然不同,可见对于配对观察数据如果按配对数据方法来分析,可以得到较精确的结论,误认为普通双样本数据来分析则容易犯第二类错误而得不到正确结论。