(1) 单比率p的显著性水平为α的检验
例5-6
某厂规定产品必须经过检验合格后才能出厂,其不合格率 p0 不得超过5%。现从一批产品中随机抽取200个进行检验,发现16个不合格品,问该批产品能否出厂?(α=0.05)
1)设H0 :p ≤ 0.05, H1 :p>0.05。
2)显著性水平 α=0.05。
用Minitab计算路径:统计-->基本统计量-->单比率。
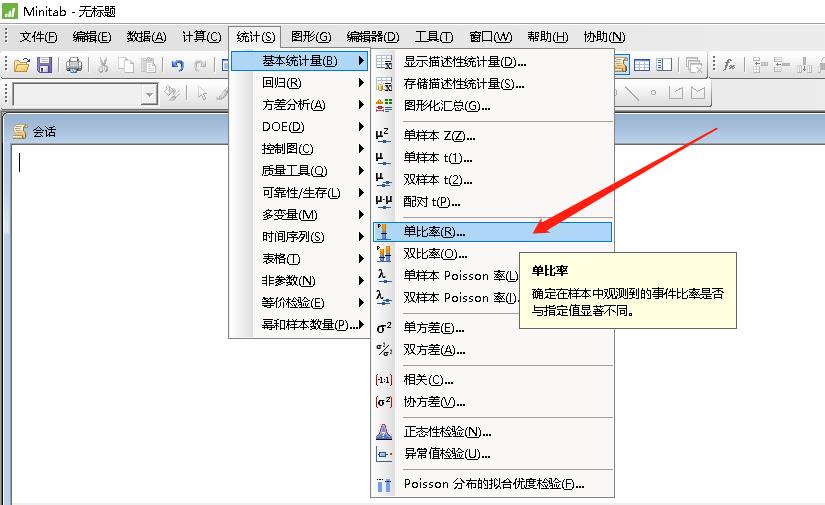
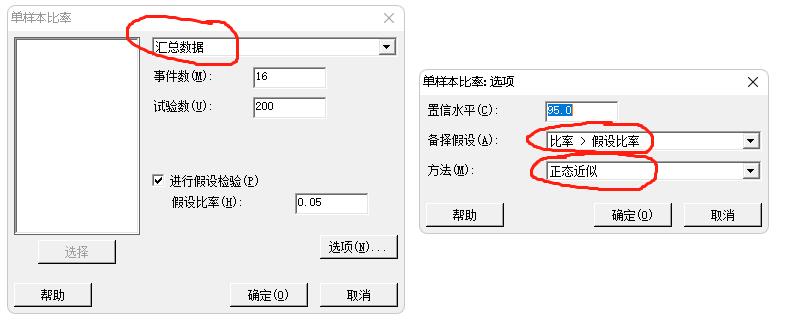
计算结果:

结果分析:
P值=0.026<0.05,所以拒绝原假设,不允许这批产品出厂。
(2)双比率、显著性水平为α的检验
例5-7
用A与B两种不同的方法制造某零件,从各自制造的零件中分别随机抽取100个,其中A方法有10个不合格品,B方法有6个不合格品。在 α=0.05的水平上,能否认为不合格率与方法有关?
解:
1)设A方法不合格品率为p1 ,B方法合格率为p2 ,假设:H0 : p1 = p2 , H1 : p1 ≠ p2 。
2)用Minitab计算的路径:统计-->基本统计量-->双比率
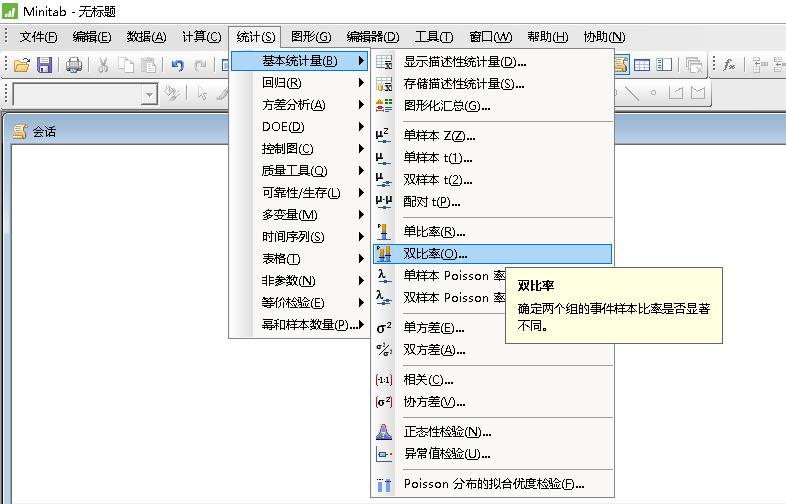
选项设置:
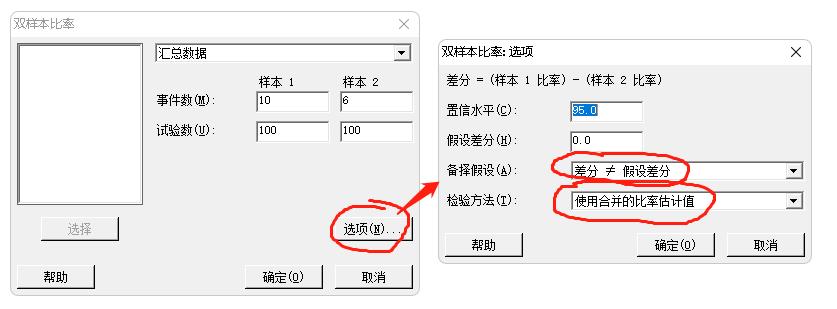
计算结果:

结果分析:
计算得P值为0.297,大于给定的 α=0.05,因此无法拒绝原假设。得出结论,两种方法无显著差异。
本例给了我们很大的启发,表面上看10%当然比6%要大,但是在样本量较小时竟然得不到有显著性差别的结论,统计工作者不应简单的相信百分数。
若将本例的数字都扩大10倍重新计算,则二者的差别如下所示就是显著的了。
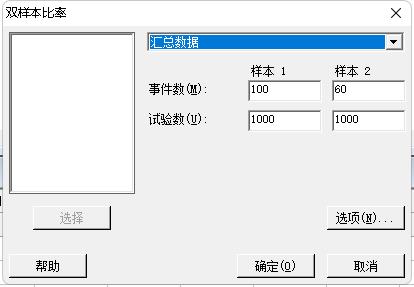
计算结果:
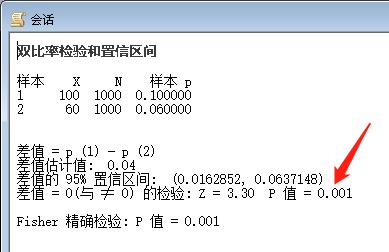
结果分析:P=0.001<0.05,拒绝原假设,两种方法有显著差异,不合格率与方法有关。