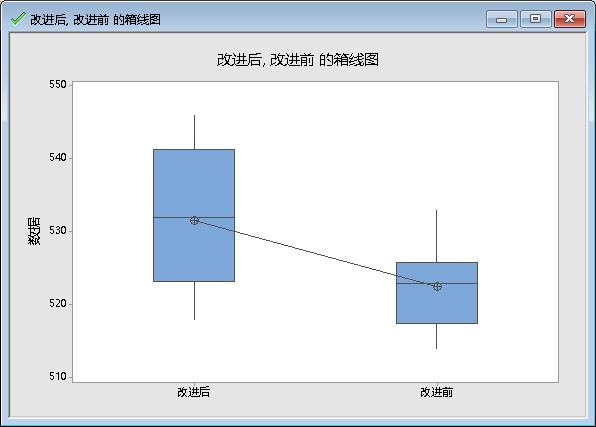
设有两个独立总体, X~N( μ1 ,σ1²), Y~N( μ2 ,σ2²), 从总体X中抽取的样本x1 , x2 ,..., xn ,样本均值为x bar,样本方差为 sx²,样本标准差为 sx 。从总体Y中抽取的样本y1 ,y 2 ,..., yn ,样本均值为y bar,样本方差为 sy²,样本标准差为 sy 。
例5-5
在改进工艺前后,分别测量了若干钢条的抗剪强度,数据如下:
改进后:525,531,518,533,546,524,521,533,545,540
改进前:521,525,533,525,517,514,526,519
问:可以认为改进工艺后钢条的平均抗剪强度有提高吗?
解:
(1)首先检验方差是否相等。
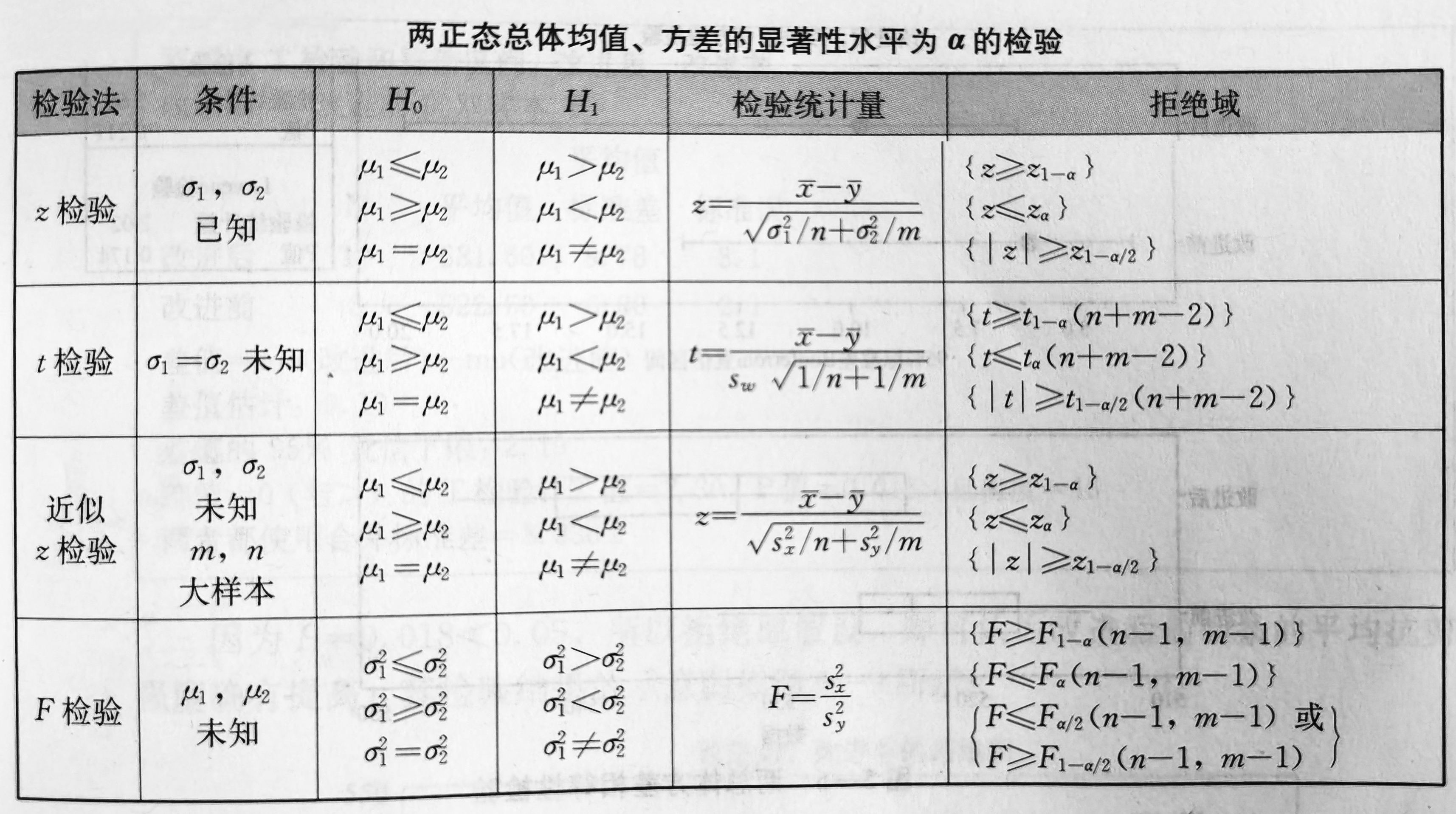
1)假设 H0 : σ1² = σ2² , H1 : σ1² ≠ σ2²
2)因方差不知故用 F 检验,显著性水平α=0.05。
Minitab计算路径:统计-->基本统计量-->双方差
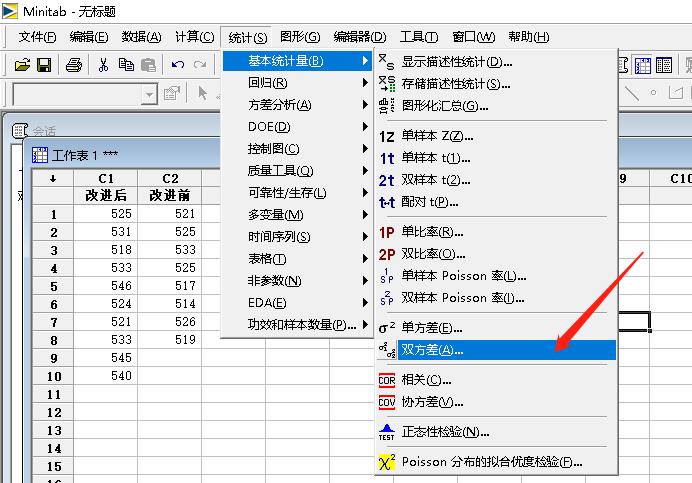
对话框和选项:
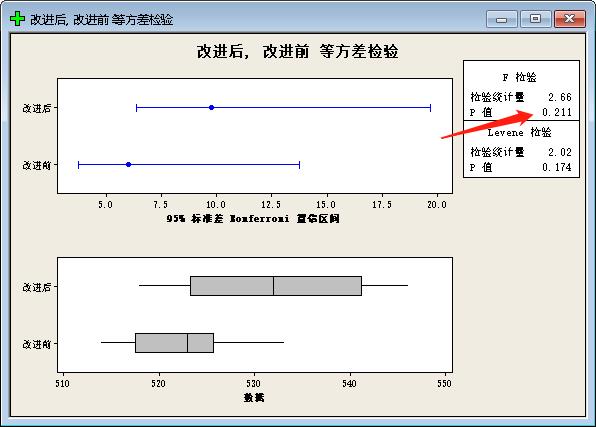
结果分析:
由于F检验 P=0.211>0.05,因此不能拒绝原假设,可以认为改进前后的方差相等。
(2)检验均值是否有提高。
1)设 H0 :μ1 = μ2 , H1 :μ1 > μ2 。
2)由于两总体方差相等,但未知,故选用 t 检验。
3)根据显著性水平α=0.05,进行Minitab运算。
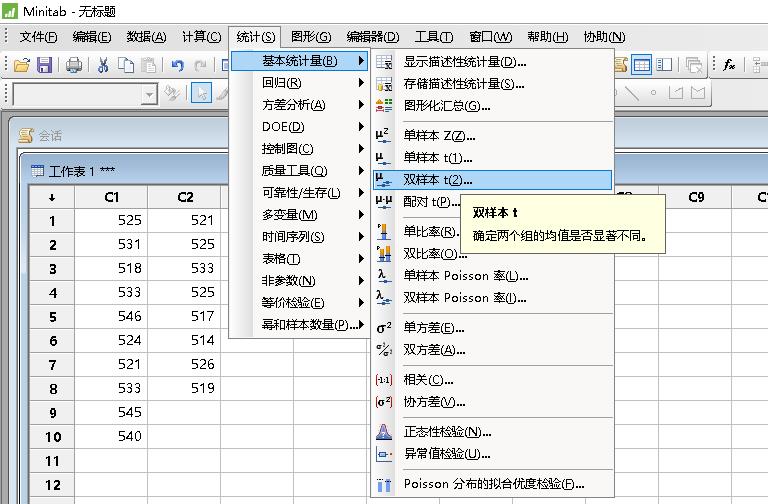
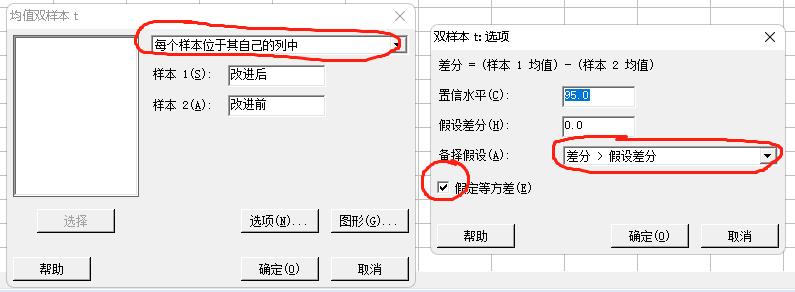
运算结果:
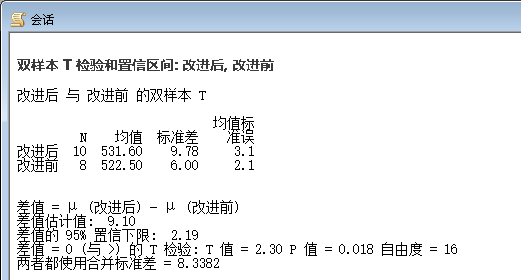
结果分析:
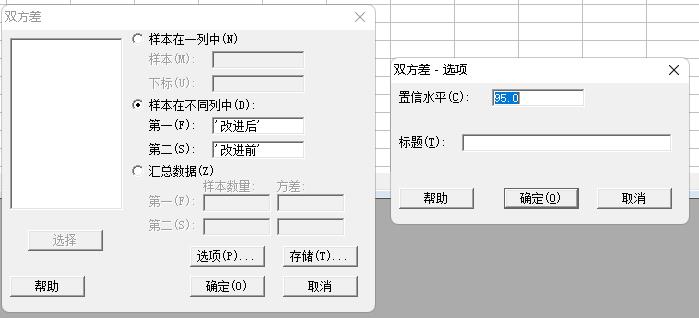
因为P=0.018<0.05,所以拒绝原假设,即可认为改进后的钢条的平均抗剪强度确有提高。
生成箱线图: