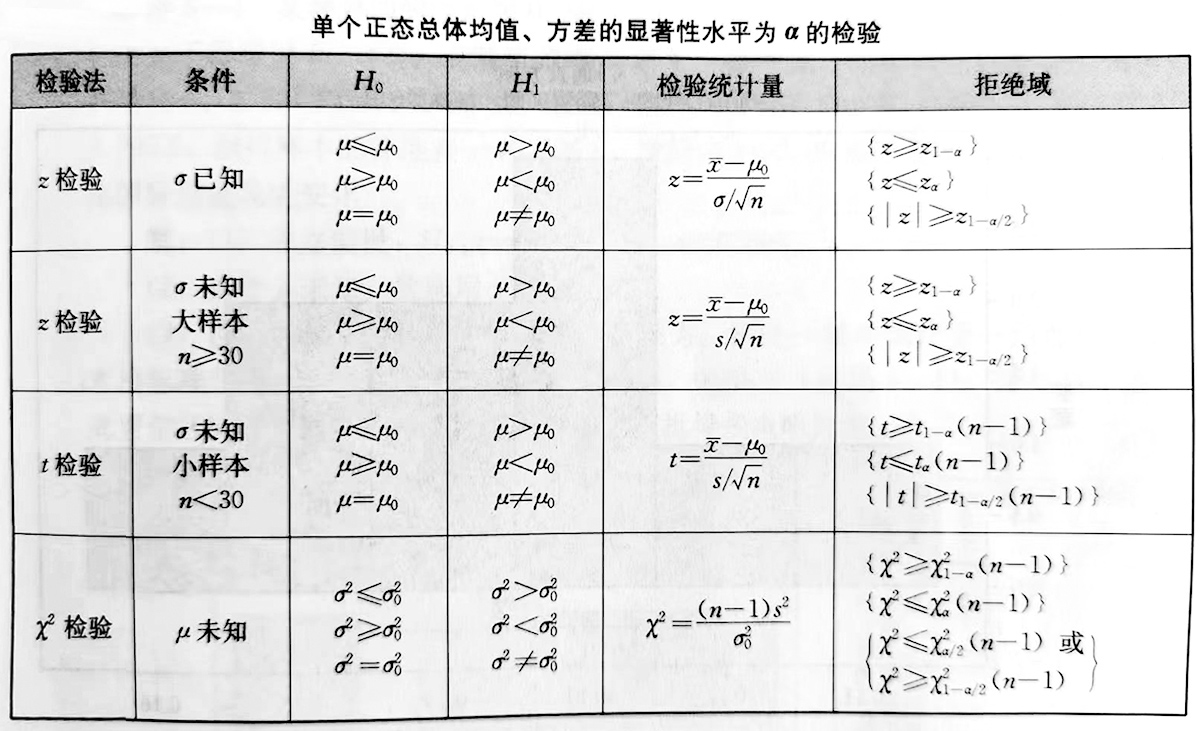
(一)单个正态总体均值、方差的显著性水平为α的检验。
设总体分布为N(μ,σ²),从总体中抽取的样本为x1,x2,...,xn,样本均值为X bar,样本方差为s²,样本标准差为s。
(1)关于μ的显著性水平α的检验。
1)当正态分布标准差σ已知时,关于正态均值μ常用的三对假设为:
H0 :μ=μ0 (或μ ≤ μ0), H1 :μ>μ0 (单边假设检验)
H0 :μ=μ0 (或μ ≥ μ0), H1 :μ<μ0 (单边假设检验)
H0 :μ=μ0 , H1 :μ≠μ0 ( 双边假设检验,即μ>μ0或μ<μ0)
检验统计量都用统计量:
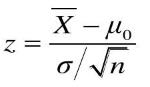
在 H0成立,即μ>μ0 时,z~N(0,1)。
给出显著性水平α,根据上述假设,分别定拒绝域W:
W = {z ≥ z1-α},W = {z ≤ zα}, W = { | z | ≥ z1-α/2}
2)当σ未知时,可以用样本标准差s代替。
● 大样本(n≥30)时,采用检验统计量
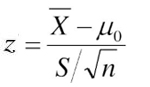
拒绝域W为:
W = {z ≥ z1-α},W = {z ≤ zα}, W = { | z | ≥ z1-α/2}
● 小样本(n<30)时,采用检验统计量
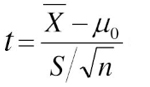
在H0成立时,t~t (n-1 )。
相应于上述三个检验问题的拒绝域W改用t分布获得,分别为:
W={t≥t1-α(n-1)},W={t ≤ tα(n-1)},W={ | t |≥t1-α/2(n-1)}
(2)关于σ²的显著性水平为α的检验。
可以采用检验统计量
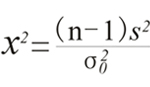
在不同的检验问题中拒绝域按不同方法确定。
例 5-2
某零件的厚度在正常生产情况下服从N(0.13,0.015² )。某日在生产的产品中抽查了10次,其观测值为:0.112,0.130,0.129,0.152,0.138,0.118,0.151,0.128,0.158,0.142。发现平均厚度已稍有变化,如果标准差不变,试问生产是否正常?(α=0.05)
解:(1)建立假设: H0 :μ=0.13 , H1 :μ≠0.13。
(2)由于标准差 σ已知,故选用 Z 检验。

(3)选择Minitab的菜单“统计--单样本Z”:
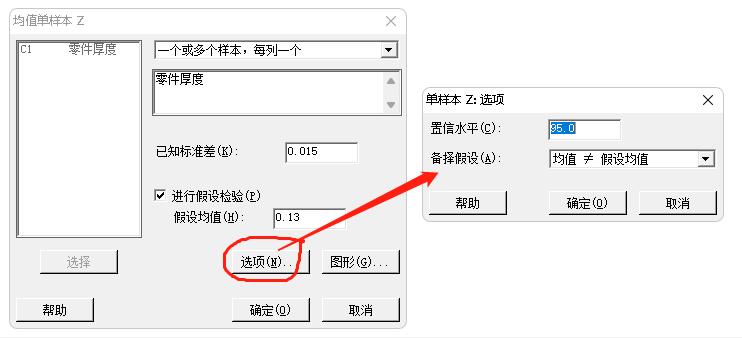
注意:“选项”对话框中的备择假设应选“均值≠假设均值”;
运算结果:
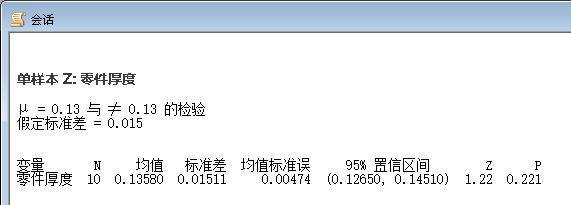
结果分析:
● 因为P=0.221>0.05,不能拒绝 H0,即认为平均厚度变化到0.136与0.13并无显著差别,即这批产品平均厚度合格。
● 由于观测的样本均值是0.136,置信区间显示。以95%的把握断言,总体均值落在(0.127,0.145),μ=0.13落入此置信区间,因此无法拒绝原假设。
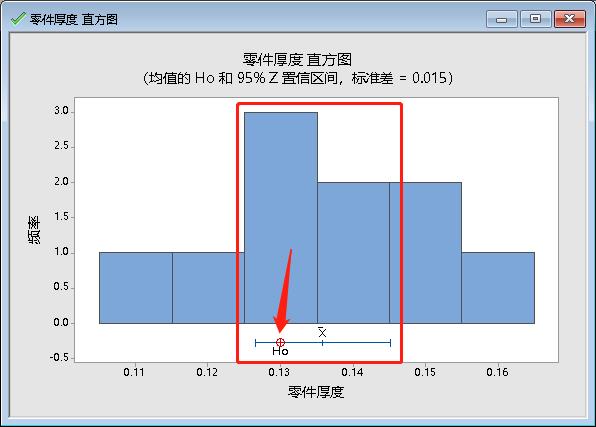
从生成的直方图直观也可以断定:
当 H0所对应的均值未落入均值的置信区间时,则拒绝原假设;否则不能拒绝原假设。本例的结论是:不能拒绝原假设 H0,即平均厚度与0.13无显著差别。
例 5-3
某宾馆六西格玛团队评定某项服务的等级,最大可能的级别为10。服务等级的总体均值“达到7”的服务项目可以接受,总体均值“超过7”的认为有提高。随机调查12位顾客,要求他们对此项服务评定等级,得到12个级别数据分别为:7,8,10,8,6,9,6,7,7,8,9,8。假设总体级别近似服从正态分布,在显著性水平α=0.05的情况下,问服务项目确实比规定的可接受标准有提高吗?
解:
(1)建立假设:: H0 :μ=7 , H1 :μ>7。
(2)如果拒绝H0,则可以认为服务项目确实比规定标准有提高。样本数小于30属于小样本,并且由于标准差 σ未知,故选用单样本 t 检验。
(3)Minitab路径:统计--基本统计量--单样本的T检验。
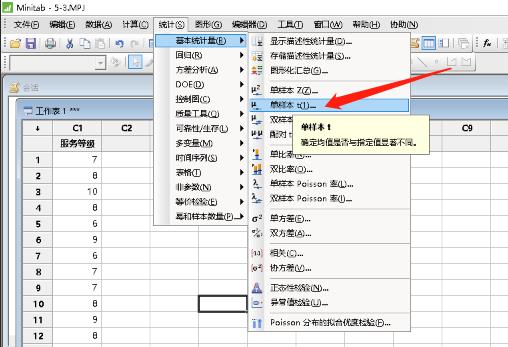
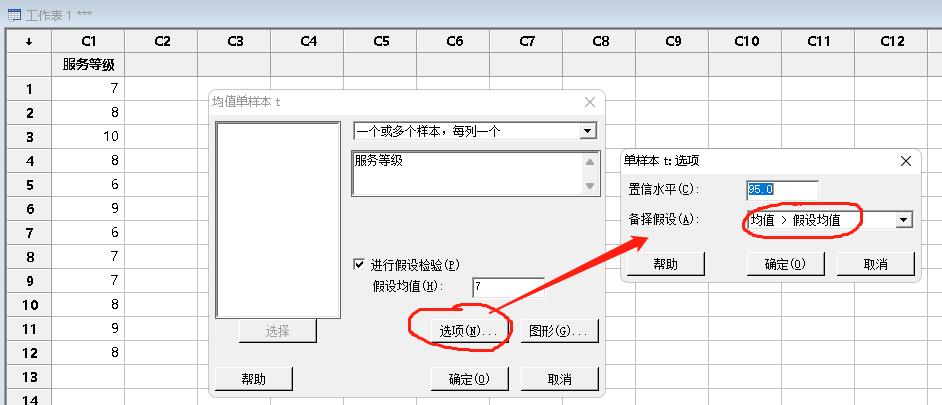
运算结果:
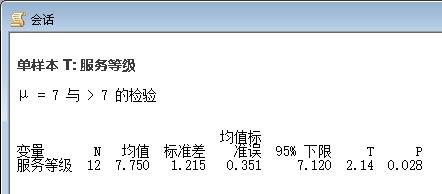
结果分析:
● P=0.028<0.05,拒绝H0,可以认定服务项目确实比规定标准有提高;
● x bar=7.750,s=1.215,t=2.14,故拒绝H0,可以认定服务项目确实比规定标准有提高。
例5-4
某种导线的电阻服从N(μ,σ²),μ未知,但要求千米导线电阻的标准差不得超过0.005Ω。现随机抽取9根千米长导线,测得其电阻数据分别为:10.0100,9.9977,9.9898,10.0008,10.0024,10.0048,9.9996,10.0078,9.9932,测得样本的标准差 s=0.0066。试问在α=0.005水平上能否认为该批导线电阻标准差发生变化?
解:
(1)建立假设:H0 : σ =0.005 , H1 : σ ≠ 0.005。
(2)由于μ未知,故选用 X² 检验。
(3)Minitab操作路径:统计--基本统计量--图形化汇总。
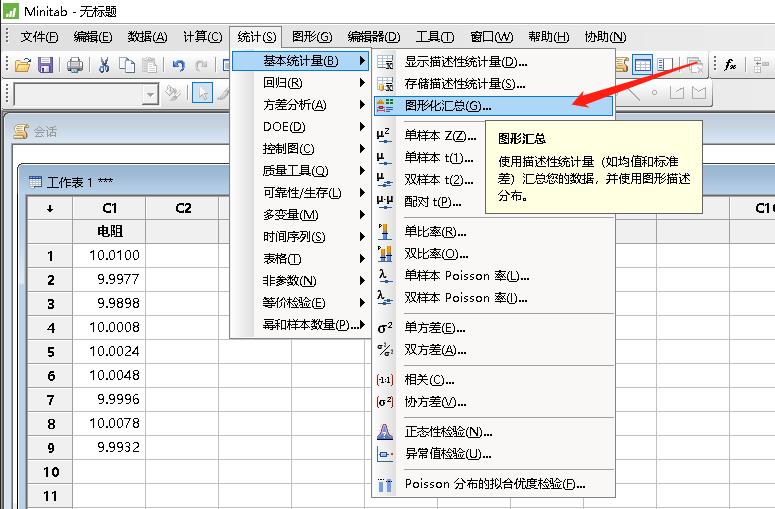
运算生成图形:
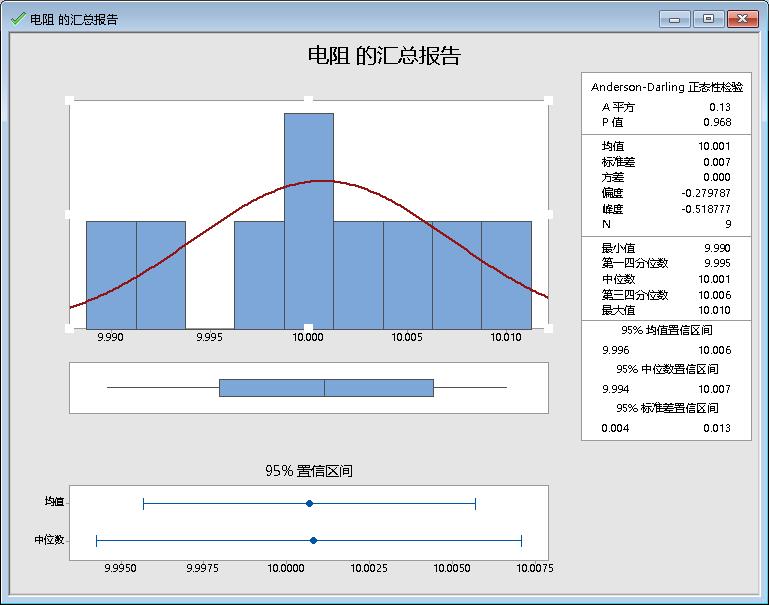
结果分析:
求出标准差的95%双侧置信区间为(0.004,0.013),而0.005落入此置信区间,因此不能拒绝原假设,认为该批导线电阻标准差合格。
一般来说,估计总体均值大约n=15就够,而估计标准差大约要n=30才能估计得比较好。本例中n=9,对于估计样本均值样本容量已经不够,当然对于估计标准差就更不够,所以才导致结果中其双侧置信区间太宽了。