实际问题都是复杂的,任何数学模型都只是它的某种抽象概括。
(1)因子:可控因子与非可控因子
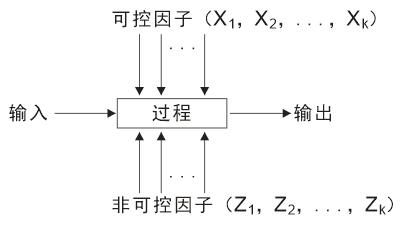
因变量Y(response):又称“响应变量”或“指标”,是我们关心的输出变量。
因子(factor):影响响应变量Y的那些自变量X称为试验问题中的因子。
可控因子:人们在试验中可加以控制的因子,它们是输入变量,是影响过程结果的。可以是连续型的(通常情况),也可以是离散型的。
非可控因子:又称噪声因子(noise factor),常被当作误差来处理。影响过程及结果的变量除了可控因子外,还可能包含一些可以记录但不可控制的非可控因因。通常很难将它们控制在某个精确值上,实际问题中它们确实也可能取不同的值,
(2)水平及处理
为了研究因子对响应变量的影响,需要用到因子的两个或更多不同的取值,这些取值称为因子的水平(level)或设置(setting)。
各因子皆选定了各自的水平后,其组合称为处理(treatment)。
按照设定的因子的水平组合,就可以进行试验了。一次试验将会得到一次响应变量的观测值,这就是一次试验(trial or experimental run),简称为一次运行(run)。
一个处理可以进行多次试验。
(3)试验单元与试验环境
试验单元(experiment unit):指对于对象、材料或在制品等载体,处理(即试验)应用于其中的最小单位。
试验环境(experiment environment):以已知或未知的方式影响试验结果的周围条件,通常包括温度、湿度、电压等。
(4)模型与误差
数学模型:
Y=∫( X1,X2,...
, XK) + ε
式中,Y是响应变量;
X1,X2,...,XK 是可控因了;∫是某个已知的确定的函数关系;ε是误差。
误差ε主要是非可控因子(或噪声)所造成的试验误差(experimental error),还包括了测量误差。
为了不使测量误差影响分析结果,通常要在试验进行前,先进行测量系统分析,只有测量误差满足了对测量系统的最低要求后,试验才能开始进行。
(5)主效应和交互效应
主效应通常指各个独立变量对因变量的独立影响,又称为“因子效应”。
如某个试验中,考虑两个因子A和B,每个因子皆有两个水平,则:
因子A的主效应 = A处于高水平时Y的平均值 - A处于低水平时Y的平均值
因子B的主效应 = B处于高水平时Y的平均值 - B处于低水平时Y的平均值
交互作用(interaction):定义两因子间有交互作用为——如果因子A的效应依赖于因子B所处的水平,则称因子A与因子B之间有交互作用(interaction)。
两因子交互效应(interaction effect)公式:
AB交互效应 = (因子B处于高水平时因子A的效应 - 因子B处于低水平时因子A的效应)÷ 2
BA交互效应 = (因子A处于高水平时因子B的效应 - 因子A处于低水平时因子B的效应)÷ 2
如果二者是相同的,不再区别A*B 或B*A。
值得注意的是,如果两个因子间存在显著的交互作用,就不能只用主效应的大小来作为该因子是否重要的判断依据。有时一个因子主效应很小,只要某个含此因子的交互作用效应显著,则这个因子就是重要的,就应予以保留。