（观看时建议屏幕最大化并关闭静音）

       定量分析方法，亦称“数量分析法”，是通过反映一定质的事物的量的关系来揭示事物内在规律性的方法。通过建立预测分析的数学模型，揭示影响预测目标各有关变量之间的规律性联系，根据求解数学模型得到的结果，进一步分析考虑相关的非定量并作出预测结论，使解决方案更加精确。

       定量分析具有探索性、诊断性和预测性等特点。

       本节课将要学习的定量分析方法有：80/20法则、ABC分析法、相关分析、数学模型等。

(一) 80/20 法则。
       又称帕累托法则、关键少数法则、二八法则。指仅有20%的因素影响80%的结果，或者说：所有变因中，最重要的仅有20%的因素影响80%的结果。

       是由十九世纪末期与二十世纪初期的意大利经济学家兼社会学家帕累托所提出的。意思指按事情的重要程度编排行事优先次序的准则，是建立在“重要的少数与琐碎的多数”原理的基础上的。

       企业中，事实上大部分的问题，只要能找出几个影响较大的因素加以处理及控制，就可以解决80%以上的问题。柏拉图最早用排列图分析社会财富分布的状况，后来美国质量管理专家朱兰博士运用柏拉图的统计图加以延伸将其用于质量管理。

80/20法则应用案例：
       柏拉图是根据归集的数据，以不良原因，不良状况发生的现象，有系统地加以项目别（层别）分类，计算出各项目别所产生的数据（如不良率，损失金额）及所占的比例，再依照大小顺序排列，再加上累积值的图形，通过柏拉图我们可以快速找出最主要是质量问题。

       LDMES系统将不良品数据由大到小排列生成柏拉图，管理人员能很直观地看到质量问题出在哪，优先采取改善措施减少主要不良品。不同工人的操作水平不一致，他们需要及时掌握本人的生产质量情况，哪类不良占多数，从而有针对性自觉提升自己的操作技能，从而快速提高自己的生产质量水平。

(二) ABC分析法。
       ABC分析法又称为重点管理法或分类管理法。其基本原理是将影响组织活动和成效的各种因素依其重要性分成A、B、C三类。ABC分析法有利于分清主次，抓住重点，区别对待。在管理能力有限的条件下，ABC分析法可以有效地控制管理方向，通常可运用于设备管理、客户管理、物料管理等。

ABC分析法案例：
        SCG公司采用ABC分析法对库存原材料进行分类管理，以便降低库存，并能保证准时提供生产线物料。在一次盘点后，依库存金额由大而小排序并进行了累计计算。经整理后制定出了如下的物料库ABC分类表：

       从库存品种ABC分级曲线图可看出，A级物资在品种数量上虽仅占6%左右，但若能管好他们，就等于管好了消耗金额90%左右的物资。具体应做到以下几点：
1) 与供应厂家密切联系，以保证生产的生常运行；
2) A级物资占金额比例最大，应该选择恰当的安全系数尽可能减少安全库存量，从而减少库存资金的占用量；
3) 考虑到A级物资在库存资金所占比例极大，应制定经济订购批量；
4) 应做好市场调研，掌握客户对该产品的需求状况，从而较为准确地制定生产计划。

        SCG电子公司制定了ABC物资管理分类表，规范了对库存物资的日常管理。对A类物资进行了严密控制，对库存量详细计算管控，对每笔进出都进行非常详细的记录，平时只有少量库存量以避免占用过多资金，并且平时要连续检查存货情况；对于B类物资采取折中方法进行管理，对于C级物资则不应投入过多的管理资源。

（三）相关分析。
        通过统计不同变的若干组相互对应的数据来确认变量之间关联程度的分析方法。

        一般变量之间的关系可分两种：确定型关系和非确定型关系。

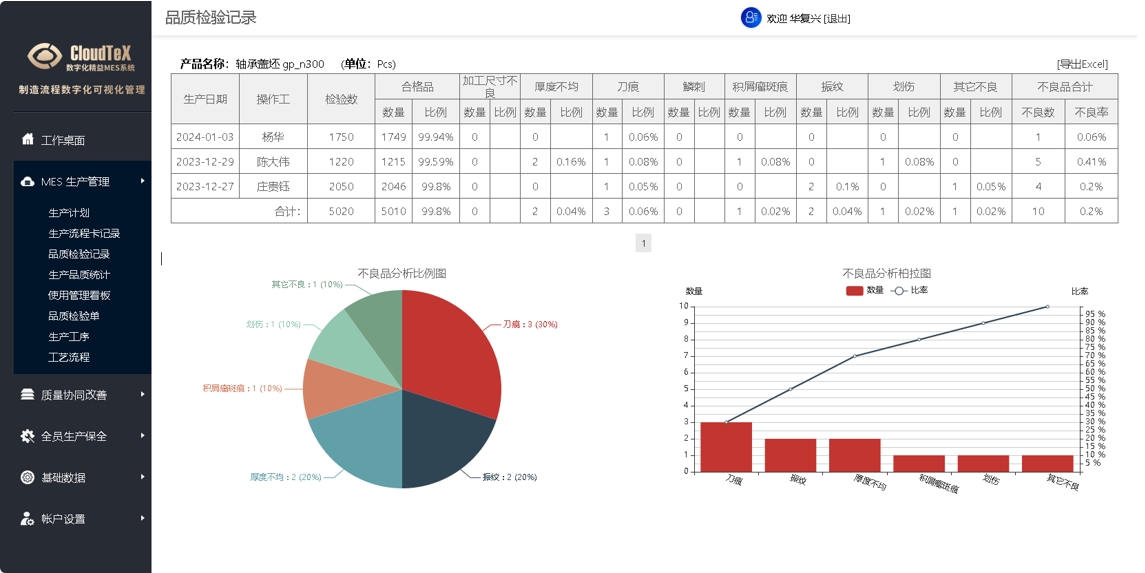
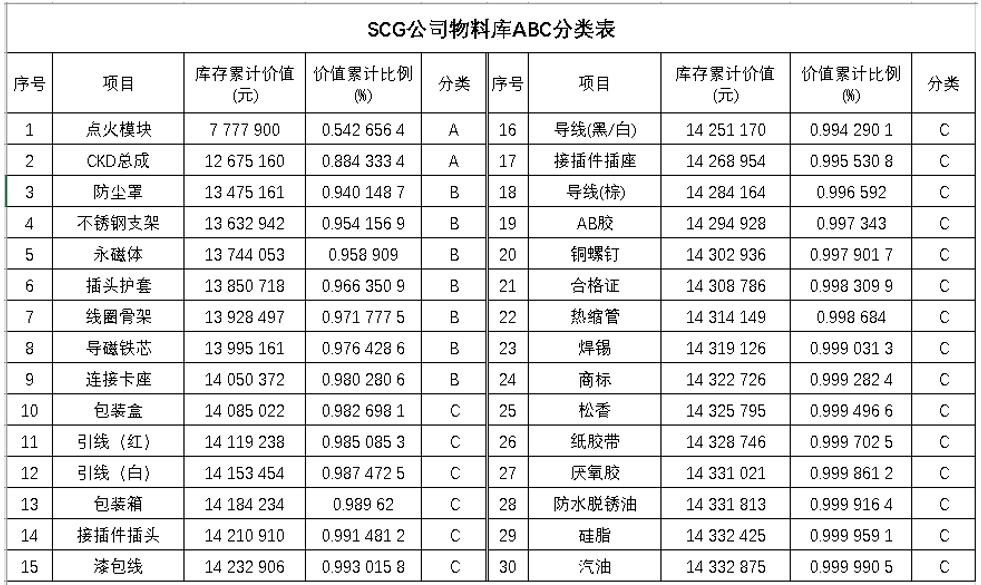
例如：
        产品价格不变前提下销售额与销售量的关系称为确定型关系，即知道了销售量就能准确地算出销售额。
虽然农作物单位面积产量与施肥量之间有一定关系，但根据施肥量来推算农作物单位面积产量却不一定准确，这种关系被称为非确定型关系。

       变量之间的关系可以用相关系数来衡量。相关系数指用来反映具备相关关系的变量间的相关程度。

       相关系数为0，两个变量之间不相关；相关系数小于0为负相关，两数据间呈反向成长；相关系数大于0为正相关，两数据间呈正向成长；当相关系数绝对值为1，则变量之间完全相关。

       常用的判定准则是：相关系数绝对值大于0.7，属于高度相关；0.3~0.7之间属于中相关；低于0.3属于低度相关。至于何种相关系数合适要视实际需要。

       有一种假相关的现象需要注意，虽然计算出有些变量之间的相关系数较高，但实际上相互之间却毫无相关。对于假相关现象，定量分析无法辩别，只能用常识或现象之间的逻辑关系来鉴别。

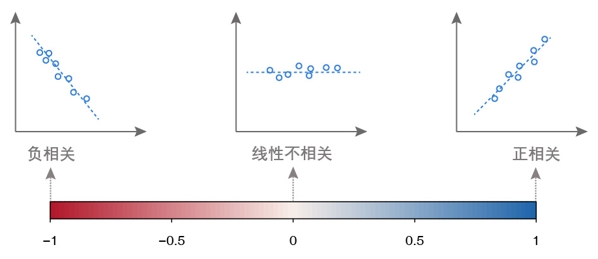
        假相关的例子如：统计研究发现，冰淇淋销量最高的时候，就是公共泳池的溺水事故发生得最多的时候。
然而，有可能热浪造成冰淇淋销量和公共泳池的溺水事故增多。若视冰淇淋的销量或遇溺事故为对方的成因，可能就被假相关关系误导了。

相关分析案例：

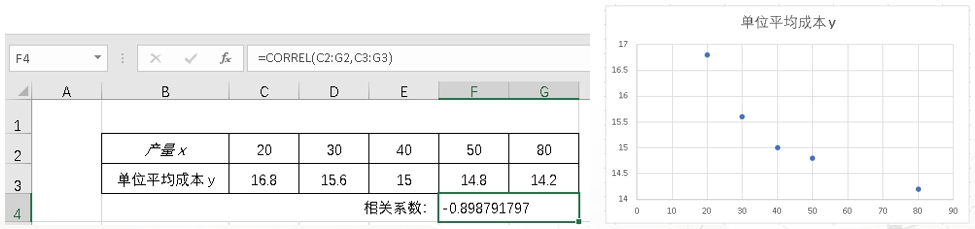
        STU公司是一家化学制品厂，公司经理想要获得产量与单位平均成本的相关系数，先是记录近期的几次不同产量的生产数据，再利用Excel的CORREL计算出相关系数为-0.8988，因此可以得到产量与平均成本两个变量属于高度负相关。从生成的散点图趋势也可以直观地反映了两个变量间的负相关关系。

（四）数学模型。
       数学模型是运用适当的数学工具得到一个数学结构，模仿或表达变量之间的数量依存关系。

       前面相关分析的案便学习中， STU公司计算出了产量与单位平均成本的相关系数为-0.8988，利用这个相关系数便能建构出一个比较简单的数学公式，也就是数学模型，这个数学模型可以为以后的生产管理提供预测或控制用途。

数学模型的作用：
       * 解释特定现象的现实状态；
       * 预测对象的未来状态；
       * 提供处理对象的最优决定或控制。

       现实中，影响生产过程输出的因素不止一个，可能是两个或者多个因素，这些因子之间还可能存在交互作用，所以，实际生产中的数学模型是复杂得多的。以后我们会在精益六西格玛课程中的假设检验和实验设计DOE章节中详细讲解。