全因子设计的分析方法是一般的试验设计分析的典型代表。共有五大步骤：

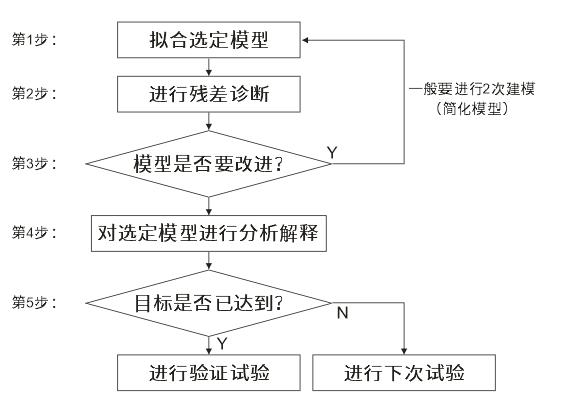
        第一步：拟合选定模型。主要任务是根据整个试验的目的，选定一个数学模型。

        通常首先可以选定“全模型”。由于三阶及三阶以上的交互作用通常都可以忽略不计，在因子设计的问题中，全模型就是在模型中包含全部因子的主效应及全部因子的二阶交互作用。在经过细致分析后，如果可以断言某些主效应及某些因子的二阶交互作用是不显著的，则在下次选定模型时，将只保留那些效应显著的项。

        Minitab软件操作 路径为  “统计-->DOE-->因子-->分析因子设计”。

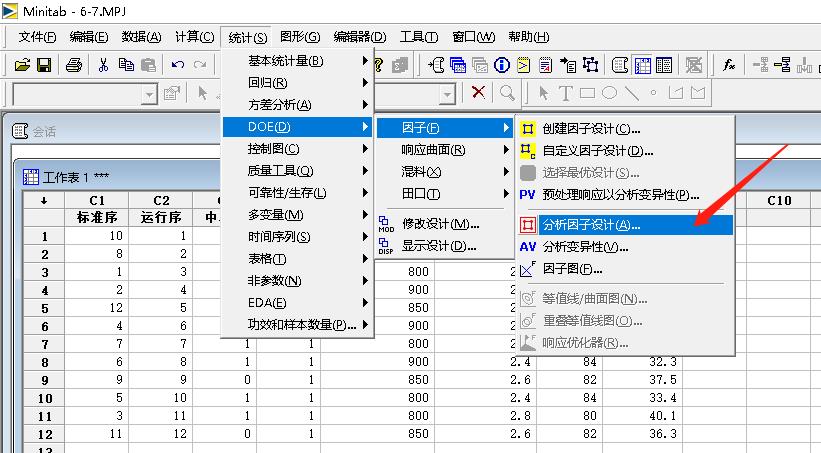
（1）ANOVA和模型整体显著性分析

        方差分析（ANOVA）是试验设计重要的分析方法。方差分析的原假设和备择假设分别是：

                    H₀  ：模型无效， H₁  ：模型有效

        如果对应回归项的P值小于0.05，则表明应拒绝原假设，即可以判定本模型总的来说是有效的。如果对应回归项的P值大于0.05，则表明无法拒绝原假设，即可以判定模型总的来说是无效的。遇到这种情况就比较麻烦，这说明模型整体似合有问题。造成这种情况的常见原因可能如下：

        1）试验误差太大。由于ANOVA检验的基础是将有关各项的离差均方和与随机误差的均方和相比较，取其比值形成 F 统计量。如分母的随机误差均方太大，则将使F变小，从而得不到“效应显著”的结论。这时，应仔细分析误差产生的各种原因，能否设法降低是找到显著因子的关键措施。当然，也有可能“试验误差太大”是测量系统不好造成的，这时就要设法改进测量系统。

        2）试验设计中漏掉了重要因子。这当然与上一项有某种关系。漏掉了重要因了必须会使试验误差增大，这时更应仔细分析因子的选定。通常在试验前考虑因子时，很难有把握说某因子重要或不重要，这时候，应该“宁多毋缺“，而不是相反。因子多选了，将来删除安很容易，一旦漏掉再想找回来就困难了。

        3）有可能是模型本身有问题。例如模型有失拟（lack of fit），或数据本身有较强的弯曲性（curvature），这时也可能导致判断为”模型无效“。

（2）ANOVA与模型失拟

        模型失拟是指拟定的模型与试验数据不能很好地拟合。如果模型中漏掉了关键因子或交互作用项，就会导致失拟。失拟的假设检验是：

                 H₀  ：无失拟， H₁  ：有失拟

        在ANOVA表中，如果失拟项的 P 值大于0.05，则表明无法拒绝原假设，即可以判定，本模型并没有失拟现象；反之，就说明模型漏掉了重要的项，应该补上。本项计算的依据是：最初是以重复试验间的差异作为试验误差的估计（pure error），将缺失的项（例如高次项、高阶交互项等）所造成的误差均方与之相比，经过 F 检验即可判明。以后，将判明为不显著的各项都归并为随机误差项，重新计算失拟荐是否显著。

（3）ANOVA与模型变曲项

        全因子设计是基于含有所有主因子和交互作用的一阶模型的，如果试验引入了中心点，中心点的试验结果对模型的主因子和交互作用项的参数估计不会有任何影响，也不会帮助估计出二次项。但是中心点的数据可以帮助分析模型的线性假设是否成立。

        关于是否存在弯曲的假设检验是：

                 H₀  ：无弯曲， H₁  ：有弯曲

        在ANOVA表中，如果弯曲项的P值大于0.05，则表明无法拒绝原假设，即可以判定模型并没有弯曲现象；反之，就说明数据呈现弯曲，而模型中并没有平方项，需要设计响应曲面模型的试验设计。

（4）拟合的总效果

        拟合的总效果可以看多元全相关系数 R² 及调整的多元全相关系数R_adj² 。

        由回归分析中的离差平方和分解公式可知：

                SS_T =SS_M  + SS_e 

        考虑在中的比例，定义

                 R²  = SS_M  /   SS_T 

        显然，此数值越接近 1 越好。容易看出，它有另一种写法：

                R²  = 1 - ( SS_e  /   SS_T )

       如果只有一个自变量，并且可以将此自变量看成是随机变量，则可以求出二者间的相关系数，则 R² 恰好就是此相关系数的平方。因此，它的含义是很容易理解的。对于多个自变量的情况，定义不变，它被推广为“多元决定系数”，仍然表示 SS_M 在 SS_T 中的比例。但它也有一个缺点：当自变量个数增加时，例如只增加一个新自变量，不管增加的这个自变量效应是否显著，  R² 都会增大一些，因而在评价是否该增加此自变量进入回归方程时，使用 R² 就没有价值了。为此，引入调整的 R² 即 R_adj²，它的定义是：

                R_adj² = 1 - （（SS_e  / (n-p) ）/ （SS_T  / (n-1) ））

        式中，n为观测值总个数；p为回归方程中的总项数（包含常数项在内）。也就是说，R_adj² 是扣除了回归方程中所受到的包含项数的影响的相关系数，因而可以更准确地反映模型的好坏。它同样越接 1 越好，而且在实际应用中，由于回归方程所含项数 p 总会大于1，因此很容易看出，R_adj² 总比 R² 要稍小一些。因此，两个模型的优劣可以从 R_adj² 与 R² 的接近程度来判断：二者之间越小则说明模型越好。我们常常比较包含所有自变量有关项的“全模型”与删去所有影响不显著的项后的“缩减模型”，看看究竟哪个更好，如果将影响不显著的项删去之后，二者更接近，则说明删去这些项确实使模型得到改进。

（5）对于 s 或 s²  的分析

        考虑所有的观测值与理论模型之间可以有误差，但总是假定，这个误差应该服从以 0 为均值，以 σ_e²  为方差的正态分布。在ANOVA表中，对应于残差误差（residual error）那行中的平均离差平方和（MSE）的数值恰好是  σ_e²  的无偏估计量，将其记为均方误差MSE（mean square of error），而这些软件会将其平方根 s 一并输出，可以认为 s 是 σ_e 的估计。粗略地说，在预测值的基础上，加减 2 倍 s，则可以得到预测值的 95%置信区间。因此这里的 s 在分析模型的好坏中起着关键作用，显然 s 越小说明模型越好。因此，比较两个模型的优劣关键的指标就可以选择 s 或  s²  ，s 越小，模型越好。