(6)各项效应的显著性
在计算结果的最开始部分,响应变量的效应和系数的估计(已编码单位)给出了各项主效应及各交互效应的数值及检验结果。这是对各项的分别的检验,很可能有些项是显著的,而另一些项不显著,将来修改模型时,应该将这些不显著项删除。这里要注意的是:如果一个高阶项(交互作用项或二次项)是显著的,则此高阶项所包含的主因子也必须被包含在模型中。例如,二阶交互作用BC项显著,则B及C这两个主效应项也一定要被包含在模型中,即使表面上看这两个主效应本身并不显著。
对于各项效应的显著性,计算机还输出一些辅助图形帮助判断的关结论。这里最重要的就是帕累托效应图(Pareto effect plot)。帕累托效应图是将各效应的 t 检验所获的 t 值作为纵坐标,按照绝对值的大小排列,根据选定的显著性水平 α ,给出 t 值的临界值,绝对值超临界值的效应将被选中。用帕累托效应图来判断因子效应的显著性是非常直观的,可以借此直观地验证数值结果。
经过上述各项计算,就完成了对数据的初步分析,即第一步拟合选定模型的任务。
第二步是进行残差诊断。主要目的是基于残差的状况来诊断模型是否合适。单纯从ANOVA表及回归系数的估计与检验两方面结果来分析整个结果是远远不够的。数学上可以举出这样的一些例子,其ANOVA表及回归系数结果完全相同,但它们的真实状况相去甚远。为了弥补第一步所得结果的不足,要进行残差的诊断。如果数据与模型的拟合是正常的,则残差应该是线性的。
如何判断残差是正常的呢?残差(residual)是观测到的响应变量与回归模型的预测值之差,并且假定残差是独立的,服从正太分布。应该观察一下,残差是否真的这样分布。如果确实是这样分布,则可以相信所选定的模型是正确的,否则就说明选定的模型不正确,要对模型进行某些修改。由于事先对选定的模型真的没有绝对把握,因此,残差诊断还是有必要的。
残差诊断应该包括四个步骤,观察计算机自动输出的四个图形。Minitab操作路径:统计-->DOE-->因子-->分析因子设计,在对话窗“图形”中选定“四合一”,再加上对各自变量的残差图就可以得到残差诊断图。
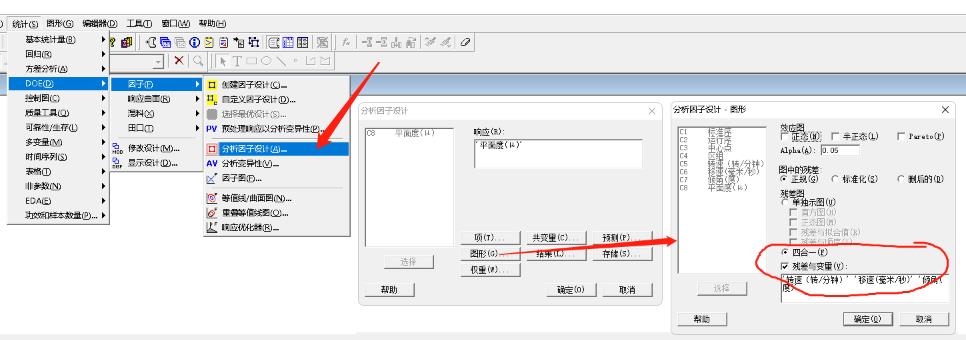
1)观察残差对于以观测值顺序为横轴的散点图:重点考察此散点图中,各点是否随地在水平轴上下无规则地波动。
2)观察残差对于以响应变量拟合预测值 为横轴的散点图,重点考察此散点图中,残差是否保持等方差性,即是否有“漏斗形”或”喇叭形“。
3)观察残差的正态性检验图(或直方图),看残差是否服从正态分布。
4)观察残差对于以各自变量为横轴的散点图,重点考察此散点图中是否有弯曲趋势。
残差诊断的四个图都应是正常的。什么是最常见的情况而被认为“不正常”呢?
异方差性是第一种最常见的残差图不正常的情况,出现在残差对响应变量拟合值的图中,残差未保持等方差,散点明显呈“漏斗形”或“喇叭形”,这说明对响应变量Y作某种变换后才会与模型拟合更好。
模型选择是第二种最常见的残差图不正常的情况,出现在残差对自变量的散点图中。残差虽保持等方差,但散点明显呈U形或反U形弯曲,这说明对响应变量Y而言,对该自变量X仅取线性项已经不够了,增加X的平方项或立方项,将会使模型拟合更好。
总之,DOE分析的第二步只是进行残差诊断,看“模型是否有问题”。如果确实发现了问题,就转入第三步。
DOE分析五步法的第三步是判断模型是否要改进。考虑采取措施的主要依据是基于数值计算及残差诊断的两方面结果。如果残差诊断的四个图都是正常的,则说明模型是正常的。因此,如果残差诊断提示,要对响应变量Y作某种变换后才行,或要增加X的平方项或立方项才会使模型拟合更好,就一定要修改模改。另外,基于各项效应及回归系数计算的显著性分析可以发现,有些主效应项或交互效应项并不显著,这些项应该从模型中删除,模型的拟合要重新进行。总之,凡是发现模型需要修改时,就要返回最初的第一步,重新建立模型,现重复前面所有步骤。
经多次反复,可以获得一个我们认为最满意的方程,将它定为选定的模型。DOE分析五步法的第四步是对选定模型进行解释, 主要是在拟合选定模型后输出更多的图形和信息,并作出有意义的解释。主要涉及下列三方面:
1)输出各因子的主效应和交互效应图。Minitab操作路径:统计-->DOE-->因子-->因子图。
应该从主效应图、交互效应图进一步确认所选中的那些主因子和交互作用项是否真的很显著,未选中的那些主因子和交互作用项是否真的不显著,从而更具体更直观地确认选定的模型。
2)输出等高线图、响应曲面图等。Minitab操作路径:统计-->DOE-->因子-->等值线/曲面图。
从等高线图、响应曲面图可进一步确认响应变量是如何受所选中的那些主因子和交互作用项的影响的,它的变化规律如何。如果目标是望大(或望小或望目),那么自变量在什么设置时,将会达到响应变量最大(最小或与目标最接近)?我们要从直观上看到整个试验 范围内的最佳值的位置。由于等高线图、响应曲面图都只能对两个自变量的情形给出,因此当自变量个数超过两个时,要分别对选定的某两个自变量作图。
3)实现最优化。按照具体问题的望大、望小或望目在数值上求出整个试验范围的最佳值。Minitab操作路径:统计-->DOE-->因子-->响应优化器。
在因子设计阶段,试验设计的主要目标是筛选变量,但实际上,根据DOE分析第一步就可以判断出哪些自变量是显著的,哪些自变量效应是不显著的,可以在使用这些信息的基础上,获得最佳值 。"响应变量优化器"(response optimizer)是个功能强大的工具,它可以自动给出最优设置。通常只要在选定响应变量后,再对最优的目标(goal)予以设定(setup)即可。
DOE分析五步法的第五步是判断目标是否已达到。这主要是将预计的最佳值 与原试验目标相比较。如果离目标比较远,则应考虑安排新一轮试验,通常是在本次获得的或预计的最佳点附近,重新选定试验的各因子及其水平,继续做因子设计(DOE)或响应曲面设计(RSM),以获得更好的结果。如果已基本达到目标,则要做验证试验以确保将来最佳条件生产能获得预期效果。试验设计大师鲍克斯有句名言:
” 所有统计模型都是错的,只不过有些模型有用罢了。“对于根据试验 数据所建立的任何统计模型是否符合实际规律,在未验证前都没有把握判断的。通常的做法是先算出在最佳点的观测值的预测值 及其变动范围,然后在最佳点做若干次验证试验(通常要3次以上)。如果验证试验结果的平均值落入事先计算好的范围内,则说明一切正常,模型是正确的,预测结果可信;否则就要进一步分析发生错误的原因,改进模型,重新验证,以求得符合实际数据的统计模型。Minitab的路径”统计-->DOE-->因子-->分析因子设计“可以得到对于指定的自变量设置计算出预测值(fits),预测值处的标准差(SEs of fits),预测值 处的回归结果的置信区间(confidence limit,输出时缩写为95%CI),预测值处的单个观测值的置信区间(prediction limit,输出时缩写为95%PI)。
前一个置信区间(95.0%CI)表明的是回归方程上的点的置信区间,这是由于回归系数是以样本观测值 为基础估计出来的,它必然会有误差,而回归系数的误差必然导致回归方程的预测值的误差。对此区间可以理解为,当按照此自变量的设置无限多次地重复运行下去将会获得的理论均值的95%置信范围,此值可以作为改进结果的预报写在总结报告中。后一个置信区间(95.0%PI)表明的是以上述回归方程上的点的置信区间为基础,加上观测值具有的方差为 σe2 的波动而给出的单个试验值的置信区。这是将来做一次验证试验时将要落入的范围,可供作验证试验 时使用。